Producto cartesiano de conjuntos es el conjunto de todas combinaciones de pares ordenados (x, y) de dos conjuntos dados, tal que el primer componente pertenece a uno de los conjuntos y el segundo componente al siguiente conjunto.
En el caso de que las combinaciones de «tríos ordenados» (a, b, c), de tres conjuntos dados, el primer componente pertenece al primer conjunto, el segundo al segundo conjunto y el tercero al tercer conjunto.
Dados dos conjuntos A y B, llamamos producto cartesiano AxB al conjunto de pares ordenados (a,b), tal que «a» ∈ A y «b» ∈ B, esto es: A×B={(a,b)|a ∈ A ∧ b ∈B}.
El producto cartesiano de dos conjuntos iguales A×B = B×A es únicamente posible si A=B. Para estos casos simplemente escribimos A×A=A². Pero cuando el producto cartesiano de tres conjuntos iguales AxBxC = AxCxB = CxBxA es únicamente posible si A = B = C.; y en estos casos simplemente escribimos AxAxA = A³.
Cardinal de un producto cartesiano de conjuntos.
El cardinal es el número de elementos de un conjunto, por tanto, el cardinal de dos conjuntos A y B denotados por n(A×B), es igual a n(A) y n(B) respectivamente, el cardinal del producto cartesiano es n(A×B) = n(A) ⋅ n(B).
_____________________________________________________
Ejemplo a) Si A = {1, 2} y B= {x, y}, determina AxB.
Asociando los elementos del primer conjunto con los elementos del segundo conjunto.
El cardinal es (2)(2) = 4 pares ordenados.
A x B = {(1, x) , (1, y) , (2, x) , (2, y)} Solución.
Ejemplo b) Si A={1,2} y B={2, 3, 4}y C = {3, 4, 6}, Halla (A ∪ B) x (B ∩ C).
Buscando el conjunto solución de (A ∪ B) x (B ∩ C):
(A ∪ B) = {1, 2} ∪ {2, 3, 4}= {1, 2, 3, 4}
(B ∩ C) = {2, 3, 4} ∩ { 3, 4, 6} = {3, 4}
Hallando el producto cartesiano de (A ∪ B) x (B ∩ C):
El Cardinal es (4)(2) = 8 pares ordenados.
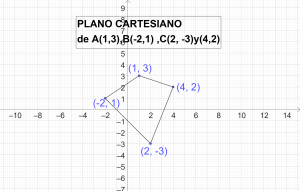
(A ∪ B) x (B ∩ C) = {1, 2, 3, 4} x {3, 4} = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4), (4, 3), (4, 4)} Solución.
Ejemplo c) Si M = {a, b, c}, N = {1, 2, 3} y Q = {x, y}, encuentra M x N x Q.
Asociando cada elemento de M con todos elementos de N y con todos los elementos de Q:
El cardinal es (3)(3)(2) = 18 tríos ordenados.
Solución:
. ¦(a, 1, x), (a, 1, y), (a, 2, x), (a, 2, y), (a, 3, x), (a, 3, y)¦
M x N x Q={(b, 1, x), (b, 1, y), (b, 2, x), (b, 2, y), (b, 3, x), (b, 3, y)}
. ¦(x, 1, x), (c, 1, y), (c, 2, x), (c, 2, y), (c, 3, x), (c, 3, y)¦
ó bien: {(a, 1, x), (a, 1, y), (a, 2, x), (a, 2, y), (a, 3, x), (a, 3, y), (b, 1, x), (b, 1, y), (b, 2, x), (b, 2, y), (b, 3, x), (b, 3, y), (x, 1, x), (c, 1, y), (c, 2, x), (c, 2, y), (c, 3, x), (c, 3, y)}
Ejercicio 19.
Dados los siguientes conjuntos:
A = {1, 2, 3}, B = {2, 4} y C = {3, 5, 6}
Revisa los siguientes productos cartesianos y verifica que el resultado del inciso 6 es igual al obtenido en el inciso 7.
1) A x B
El cardinal es (3)(2) = 6 pares ordenado.
A x B = {1, 2, 3} x {2, 4} = {(1, 2), (1, 4), (2, 2), (2, 3), (3, 2), (3, 4)} Solución.
2) A x C
El cardinal es (3)(3) = 9 pares ordenados.
A x C = {1, 2, 3} x {3, 5, 6 } = {(1, 3), (1, 5), (1, 6), (2, 3), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6)} Solución.
3) B x C
El cardinal es (2)(3) = 6 pares ordenados.
B x C = {2, 4} x {3, 5, 6} = {(2, 3), (2, 5), (2, 6), (4, 3), (4, 5), (4, 6)} Solución.
4) B x A
El cardinal es (2)(3) = 6 pares ordenados.
B x A = {2, 4} x {1, 2, 3} = {(2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3)} Solución.
5) C x B
El cardinal es (3)(2) = 6 pares ordenados.
C x B = {3, 5, 6} x {2, 4} = {(3, 2), (3, 4), (5, 2), (5, 4), (6, 2), (6, 4)} Solución.
6) A x (B x C)
El cardinal es (3)(2)(3) = 18 tríos ordenados.
A x (B x C) = (1, 2, 3) x [(2, 4) x (3, 5, 6)] = {1, 2, 3} x [(2, 4) x (3, 5, 6)] = {1, 2, 3} x {(2, 3), (2, 5), (2, 6), (4, 3), (4, 5), (4, 6)}=
= { (1, 2, 3), (1, 2, 5), (1, 2, 6), (1, 4, 3), (1, 4, 5), (1, 4, 6), (2, 2, 3), (2, 2, 5), (2, 2, 6), (2, 4, 3), (2, 4, 5), (2, 4, 6), (3, 2, 3), (3, 2, 5), (3, 2, 6), (3, 4, 3), (3, 4, 5), (3, 4, 6)} Solución.
7) (A x B) x C
El cardinal es (3)(2)(3) = 18 tríos ordenados.
(A x B) x C = [({1, 2, 3} x {2, 4}) x {3, 5, 6}]= {(1, 2), (1, 4), (2, 2), (2, 4), (3, 2), (3, 4)} x {3, 5, 6}=
= { (1, 2, 3), (1, 2, 5), (1, 2, 6), (1, 4, 3), (1, 4, 5), (1, 4, 6), (2, 2, 3), (2, 2, 5), (2, 2, 6), (2, 4, 3), (2, 4, 5), (2, 4, 6), (3, 2, 3), (3, 2, 5), (3, 2, 6), (3, 4, 3), (3, 4, 5), (3, 4, 6)} Solución.
El resultado de los incisos 6) y 7) , tienen los mismos pares ordenados, por tanto, son iguales.
___________________________________________________
8) (A ∪ B) x (A ∩ C)
(A ∪ B) x (A ∩ C) = ({1, 2, 3} ∪ {2, 4}) x ({1, 2, 3} ∩ {3, 5, 6}) = {1, 2, 3, 4} x {3} =
= {(1, 3), (2, 3), (3, 3), (4, 3)} Solución.
En este caso, como (A ∪ B) tiene 4 pares ordenados y (A ∩ C) tiene 1 par ordenado; el cardinal es (4)(1) = 4.
__________________________________________________
9) (A – B) x C
(A – B) x C = ({1, 2, 3} – {2, 4}) x {3, 5, 6} = {1, 3} x {3, 5, 6}=
= {(1, 3), (1, 5), (1, 6), (3, 3), (3, 5), (3, 6)} Solución.
En este caso, como (A – B) tiene 2 pares ordenados y C tiene 3 elementos; el cardinal es (2)(3) = 6 pares ordenados.
__________________________________________________
10) (A – C) x (A ∩ C)
(A – C) x (A ∩ C) = ({1, 2, 3} – {3, 5, 6}) x ({1, 2, 3} ∩ {3, 5, 6})= {1, 2} x {3}=
= {(1, 3), (2, 3)} Solución.
En este caso, como (A – C) tiene 2 pares ordenados y (A ∩ C) tiene 1 par ordenado; el cardinal es (2)(1) = 2.
________________________________________________











 ,
, 
 ,
, 
 ,
, 
 ,
, 


 ,
,